Tablas de Contingencia. Partiendo de una base de datos (III)
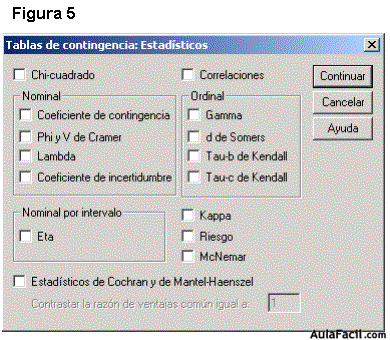
La opción de “Estadísticos” presenta una serie de coeficientes, que es necesario estudiar detenidamente. Cada uno de los coeficientes mide el grado de independencia o asociación que existe entre las variables.
En el caso de variables cualitativas la falta de independencia suele denominarse asociación, y el análisis del grado de asociación entre variables cualitativas tiene fuerte incidencia en la estadística de atributos. Se dice que dos atributos A y B son independientes cuando entre ellos no existe ningún tipo de influencia mutua.
Para medir los grados de asociación se han ideado diversos procedimientos, denominados coeficientes de asociación, entre los que destacaremos los siguientes:
· Coeficiente de contingencia C de K. Pearson: Tiene un campo de verificación de entre 0 y 1. Una relación perfecta ocurre cuando este coeficiente se iguala a 1, en tanto que en 0 se dice que las variables investigadas son independientes.
· Coeficiente T de Tschuprow: igualmente varía de 0 a 1.
· Coeficiente V de Cramer: se trata de un coeficiente que toma el valor de 1 cuando existe asociación perfecta entre atributos, cualquiera que sea el número de filas y columnas de la tabla de contingencia analizada.
· Coeficiente Lambda de Goodman y Kruskall: Suponiendo que se ha elegido Y como factor explicado y X como explicativo, se evalúa la capacidad de X para predecir Y mediante el coeficiente λx. Tanto λx como λy varían entre 0 y 1 y están especialmente pensadas como medidas asimétricas. Si λ se aproxima a 1 existe asociación entre X e Y, y se se aproxima a cero existirá independencia.
· Coeficiente Gamma de Goodman y Kruskall: Se basa en la relación relativa que siguen los rangos de dos atributos expresados en escala ordinal. La perfecta asociación positiva se da cuando y=1. La perfecta asociación negativa cuando y=-1, y la independencia de valores se da cuando y=0. La asociación será tanto mayor cuanto más se aproxime “y”, en valor absoluto, a la unidad (-1<=y<=1).
· Coeficiente de correlación de rangos de Kendall: Se trata de medidas de asociación para factores ordinales. La perfecta asociación positiva se da cuando ta=1. La perfecta asociación negativa se da cuando ta=-1, y la independencia se da cuando ta=0. La asociación será tanto mayor cuanto más se aproxime ta en valor absoluto, a la unidad.
· Coeficiente “d de Somers”: La perfecta asociación positiva se da cuando d=1, asociación negativa cuando d=-1, y la independencia se da cuando d=0. La asociación será tanto mayor, cuánto más se aproxime d, en valor absoluto, a la unidad.
· Coeficiente Eta: se utiliza cuando el atributo dependiente se mide en un intervalo y el atributo independiente se mide en una escala ordinal o nominal. El rango se mide igual que los coeficientes anteriores, 1 para una relación perfecta, y 0 cuando existe independencia de variables.
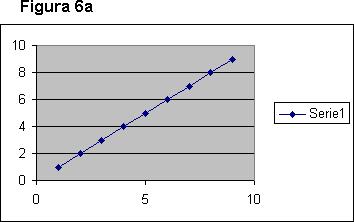
Para ejemplificar lo anterior, se presentan a continuación las figuras 6.a y 6.b. En la figura 6.a puede observarse una relación perfecta positiva, que medida en términos de coeficientes se expresaría con un (1).
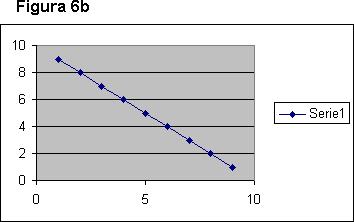
La figura 6.b muestra una relación perfecta entre las variables, solamente que en este caso, la relación es inversa o negativa, de tal forma que se expresaría con un (–1).
Si la nube de puntos se encuentra muy dispersa, y no se observa ninguna relación entre las variables, en este caso es cuando se obtienen coeficientes de asociación iguales a cero (0).