21ª CLASE
Ejercicios

22ª CLASE
Probabilidad condicionada

23ª CLASE
Probabilidad compuesta

24ª CLASE
Teorema de la probabilidad total

Vamos a analizar ahora que ocurriría con el cálculo de las combinaciones, de las variaciones o de las permutaciones en el supuesto de que al formar los subgrupos los elementos pudieran repetirse.

Por ejemplo: tenemos bolas de 6 colores diferentes y queremos formar subgrupos en los que pudiera darse el caso de que 2, 3, 4 o todas las bolas del subgrupo tuvieran el mismo color. En este caso no podríamos utilizar las fórmulas que vimos en la lección anterior.

a) Combinaciones con repetición:

Para calcular el número de combinaciones con repetición se aplica la siguiente fórmula:

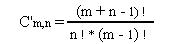
Ejemplo: C'10,4 son las combinaciones de 10 elementos con repetición, agrupándolos en subgrupos de 4, en los que 2, 3 o los 4 elementos podrían estar repetidos:

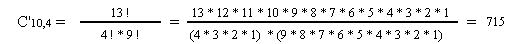
Es decir, podríamos formar 715 subgrupos diferentes de 4 elementos.

b) Variaciones con repetición:

Para calcular el número de variaciones con repetición se aplica la siguiente fórmula:

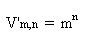
Ejemplo: V'10,4 son las variaciones de 10 elementos con repetición, agrupándolos en subgrupos de 4 elementos:

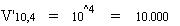
Es decir, podríamos formar 10.000 subgrupos diferentes de 4 elementos.

c) Permutaciones con repetición:

Para calcular el número de permutaciones con repetición se aplica la siguiente fórmula:

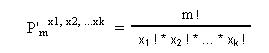
Son permutaciones de "m" elementos, en los que uno de ellos se repite " x1 " veces, otro " x2 " veces y así ... hasta uno que se repite " xk " veces.

Ejemplo: Calcular las permutaciones de 10 elementos, en los que uno de ellos se repite en 2 ocasiones y otro se repite en 3 ocasiones:

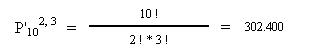
Es decir, tendríamos 302,400 formas diferentes de agrupar estos 10 elementos.

Clase anterior

Proxima clase