Poliedros
La palabra poliedro está compuesta por dos palabras griegas poli (muchos) y edro(planos, caras).
Los poliedros son cuerpos geométricos cerrados por polígonos. Estos polígonos pueden ser triángulos, cuadrados, rectángulos, etc.
Ejemplos de poliedros:
La siguiente figura es un poliedro:
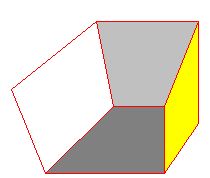
Puedes comprobar que está formada por varias caras.
Las caras son polígonos.
Aristas en un poliedro:
Arista de un poliedro es la línea donde se cortan dos caras, o si quieres, la recta que es común a dos caras (las tienes en azul en las siguiente figura):
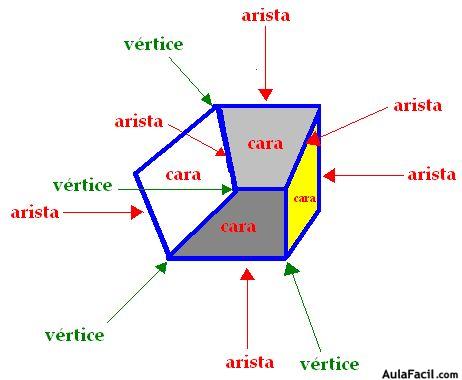
Vértices en un poliedro:
El vértice es el punto común a tres o más planos o caras de un poliedro.
Con dos caras sería imposible dibujar un poliedro y tampoco con más de cinco caras porque la suma de los ángulos interiores de los polígonos regulares que se juntan en un vértice deben valer menos de 360º.
¿Por qué?
Toma una hoja de papel y traza cuatro rectas concurrentes en un punto, tal como lo tienes en la siguiente figura:
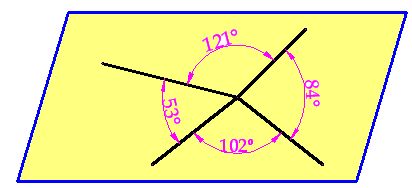
Por supuesto que no hace falta que los ángulos tengan las mismas medidas.
Tanto en esta figura como la que has realizado en el papel, la suma de los 4 ángulos es 360º.
Si ahora doblas el papel por las líneas para elevar el ángulo y así crear un volumen, verás que no se puede crear el ángulo poliedro.
En la figura (A) siguiente:
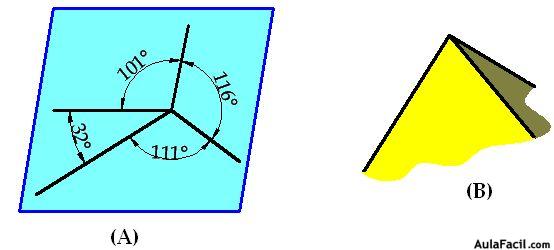
si eliminas el ángulo de 32º si puedes construir el ángulo poliedro tal como lo tienes en (B).
Para que se ajusten debidamente las caras han de sumar menos de 360º.
Los poliedros se dividen en dos grupos: Regulares e Irregulares.
POLIEDROS REGULARES
Se llama poliedro regular al cuerpo geométrico cerrado cuyas caras son polígonos regulares iguales y en el que en cada vértice se encuentran el mismo número de caras.
¿CUÁNTAS CARAS PUEDEN CORTARSE EN EL VÉRTICE DE UN POLIEDRO REGULAR?
Ten en cuenta que todas las caras de un poliedro regular han de ser iguales.
Pueden ser triángulos equiláteros, cuadrados y pentágonos regulares.
Para construir un ángulo poliedro necesitas un mínimo de 3 caras iguales y cada una debe valer menos de 120º para que entre las tres, no lleguen a 360º.
El máximo de caras iguales que se necesitan para formar un ángulo poliedro regular serían 5. ¿Por qué?
Supongamos que las caras son triángulos equiláteros iguales. Cada ángulo del triángulo equilátero vale 60º y no puede valer menos porque entre los 3 ángulos no llegarían a 180º y la suma de los ángulos interiores de todo triángulo debe valer 180º.
Si el número de caras de un ángulo de un poliedro regular fuesen 6, el producto de 60º de cada cara por las 6 caras obtendríamos 360º y no existe un ángulo poliedro de este valor, por eso, el máximo de caras han de ser 5.
Poliedros formados con triángulos equiláteros:
El menor número de caras que concurren en un ángulo poliedro ha de ser 3 y para que la figura esté completamente cerrada necesitamos 4 caras:
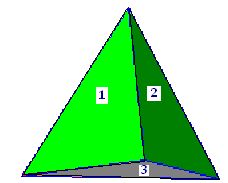
A este poliedro le llamamos TETRAEDRO: (Tetra = cuatro, edros = caras).
Las caras las tenemos numeradas, la 4ª cara no la vemos por encontrarse oculta por detrás.
Construir un tetraedro:
Necesitas: una regla, una cartulina, unas tijeras y pegamento.
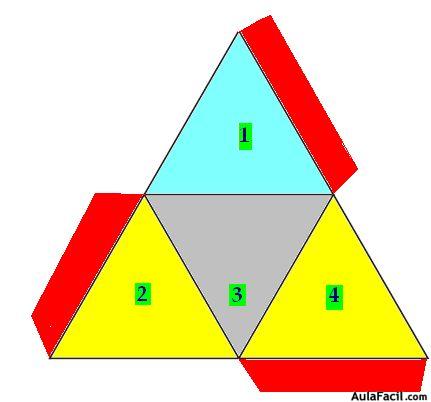
1º.- Dibuja 4 triángulos equiláteros tal como los tienes en la figura dejando tres trozos, en color rojo.
2º.- Recorta todo el contorno (respetando las solapas en color rojo).
3º.- Dobla la cartulina por las líneas en color negro. Dobla las solapas y pégalas por la parte posterior del tetraedro.
15(3).6 ¿Cuántos vértices tiene un tetraedro?
Respuesta: 4 vértices
15(3).7 ¿Cuántas aristas tiene un tetraedro?
Respuesta: 6 aristas
15(3).8 ¿Cuántas caras concurren en un vértice del tetraedro?
Respuesta: 3 caras

