Función de Proporcionalidad Directa

Cuando las variables independiente y dependiente son proporcionales, es decir cuando aumenta la variable independiente la variable dependiente lo hace en la misma proporción, y cuando disminuye la variable independiente la variable dependiente lo hace también en la misma proporción, entonces la función que las relaciona se dice que es de proporcionalidad directa.

Ejemplo: supongamos la función y = 2x

 

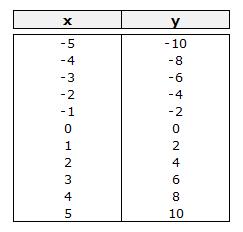
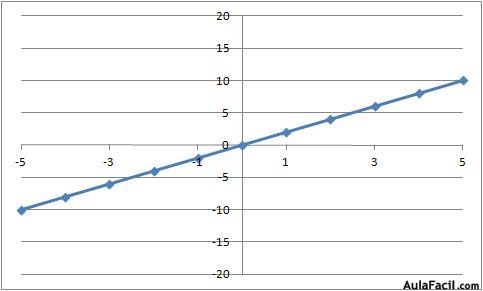
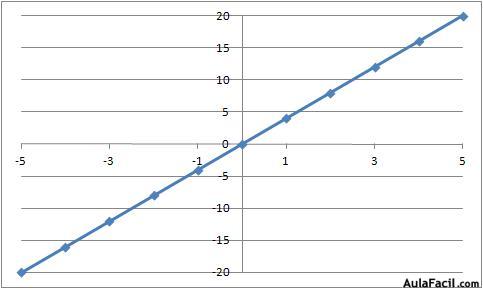
Este tipo de funciones en los que la variable dependiente es igual a la variable independiente multiplicada por un coeficiente, su representación gráfica es una recta.

La pendiente de la recta es igual al coeficiente de la variable independiente.

En el ejemplo, este coeficiente es el 2, luego la variable dependiente se incrementa (o disminuye) el doble de lo que lo haga la variable independiente.

Si el coeficiente es mayor la pendiente de la recta aumenta, si es menor la pendiente disminuye.

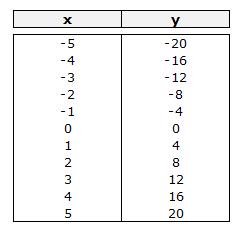
Ejemplo con y = 4x

 

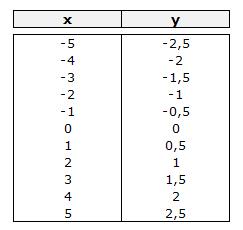
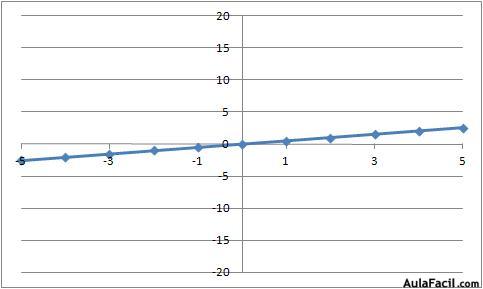
Ejemplo con y = 0,5x

 

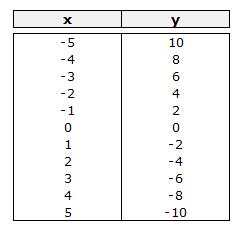
Si este coeficiente tiene valor negativo la pendiente es negativa, por lo que sería una recta decreciente.

Ejemplo con y = -2x

(pendiente = -2)

 

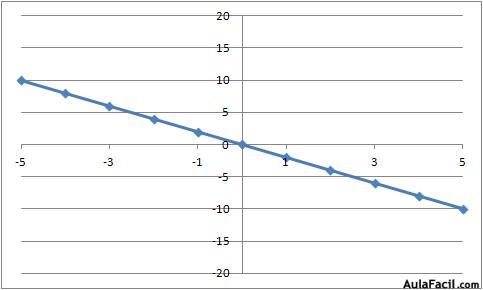
Si la función no lleva término independiente la recta pasa por el origen de coordenadas. Tal como hemos visto en los ejemplos anteriores.

Si la función lleva un término independiente, por ejemplo y = 2x + 5, la representación gráfica también es una recta pero no pasa por el punto de coordenadas sino que corta el eje vertical en el valor del término independiente, en este caso en el punto 5 (para x = 0, y = 5).

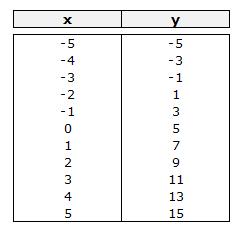
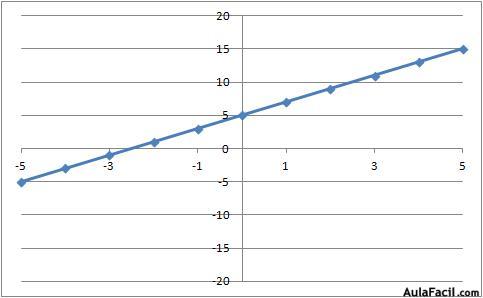
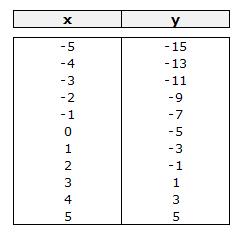
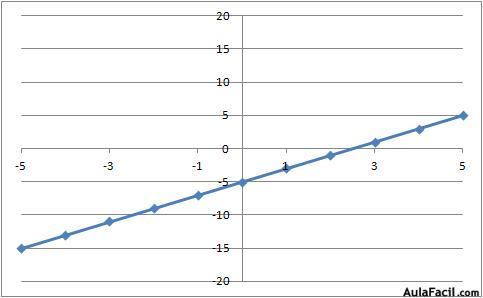
Ejemplo con y = 2x - 5

 

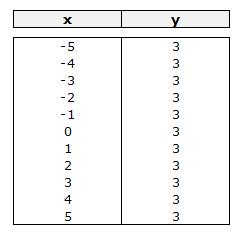
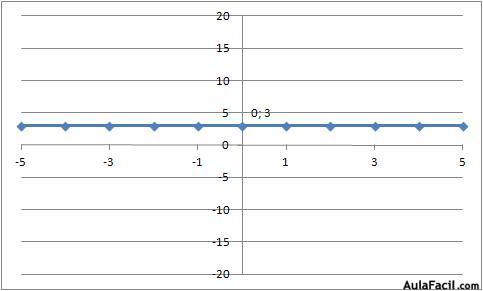
Si la función es del tipo y = 3, quiere decir que el valor de y no depende de la x, sino que siempre vale 3, con independencia del valor que tome la x. Su representación es una línea horizontal que corta el eje vertical por el punto 3.

Calcular la función de una recta

De igual manera que a partir de la función podemos calcular los pares de valores que definen la recta. A partir de un par de punto podemos deducir la función que origina dicha recta.

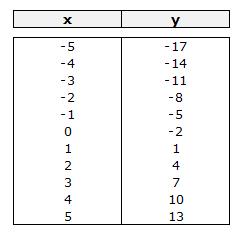
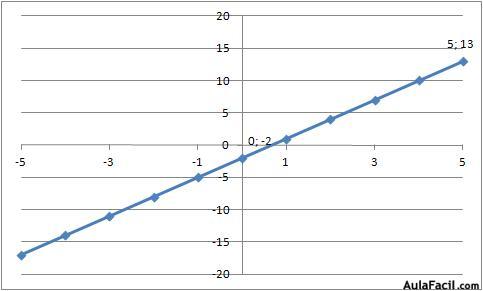
Por una parte sabemos que cuando x=0, y =-2, luego el término independiente es -2.

Por otra parte podemos calcular la pendiente o coeficiente de la variable independiente:

Si x=0, y =-2

Si x = 5, y=13

Es decir, que si “x” se incrementa en 5 (pasa de 0 a 5), “y” se incrementa en 15 (pasa de -2 a 13), luego la pendiente es igual:

Pendiente = Incremento“y” / Incremento “x” = 15 / 5 = 3

Luego la función que define esta recta es: y = 3x – 2