c) Razones estándar o razones medias

Son medidas generales de eficiencias que permiten determinar las desviaciones de las situaciones reales en base a su comparación.

La razón estándar es igual al promedio de una serie de cifras o razones simples de Estados Financieros de la misma empresa a distintas fechas o período, o bien, al promedio de una serie de cifras o razones simples de estados financieros a la misma fecha o período de distintas empresas dedicadas a la misma actividad.

Estas razones se pueden clasificar en Internas y Externas. Las primeras se obtienen de datos internos, o sea los proporcionados por la misma empresa tomando como base los años anteriores. Las segundas se obtienen tomando como referencia otras empresas similares las cuales de reunir las siguientes características:

Homogeneidad en cuanto al tipo de productos, tipo de operaciones Financieras, misma distribución y unidad de empaque.

Uniformidad en los datos: en la base de sus cálculos de costos, sus Registros contables y la presentación de su información financiera.

Podemos resumir que las razones externas estándar serán más significativas, entre mayor similitud se encuentre entre las empresas, sobre todo lo derivado a que nuestra competencia.

El método de establecer razones media estándar es el que tiene como propósito comentar a los directores de las empresas las desviaciones a los parámetros estándares previamente definidos, o sea que se realizará una administración por excepción.

c.1 Principales medidas estándar para analizar razones

Media o promedio aritmético

Se aplica para calcular el valor promedio de cantidades a cada uno de los cuales está asociado un número o peso que la pondera.

X= t/n

t= Sumatoria de la Variable

n= Número de elementos (o años)

Mediana

La mediana es un valor de la variable X que deja por debajo de él un número de casos iguales que queda por encima, o bien es un valor de posición que divide una serie de casos en dos partes iguales, cada uno con el 50%.

X= (n+1)/2

Su cálculo es simple, el número de elementos más uno, y esto se divide entre dos.

Moda

Es la medida estadística que se define como el dato o valor que más se repite en el conjunto o serie de formación. Su determinación depende de la observación.

Media armónica

Se emplea la media armónica para obtener un valor representativo de un conjunto de datos expresados en forma de tasas, esto es, tantas unidades de un tipo por cada unidad de otras especies.

La media armónica se define por X=n/(1/R):

X = n

1/R

Es decir, el valor reciproco de la media armónica de una variable positiva es igual a la media aritmética de los valores recíprocos de la variable.

Media geométrica

Hay dos usos principales de la media geométrica: 1) para promediar porcentajes, índices y cifras relativas; y 2) para determinar el incremento porcentual promedio en ventas, producción u otras actividades o series económicas de un periodo a otro.

La media geométrica (M.G.) de un conjunto de n números positivos se define como la raíz enésima del producto de los n números. Por tanto, la fórmula para la media geométrica es:

M.G. =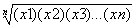

Nota: Si uno de los números es cero o negativo, no se puede calcular la media geométrica.

c.2 Problemas que presenta las razones estándar.

Las variaciones en los estados financieros de un grupo o rama de empresas y por lo tanto son sus razones, pueden que sean el resultado de uno o más de los factores siguientes:

•  Ubicación geográfica diferente por los costos de operación sean distintos.

•  Operación con bienes propios arrendados.

•  utilización de equipo nuevo o antiguo, que afecte la calidad del producto.

•  Fabricación de uno o varios productos.

•  Adecuada utilización de la capacidad instalada de la fábrica.

•  compra o producción de las materias primas.

•  Volúmenes altos de inventarios o políticas de compra consumo inmediato.

•  Sistema de valuación de inventarios diferentes (UEPS, PEPS, PROMEDIO).

•  Política de ventas distintas (sólo contado o crédito).

•  Política de compras (uno o varios proveedores).

•  Ventas con exclusividad a un cliente.

•  Determinación de capital de trabajo a utilizar.

Ejemplos de Razones Estándar

Lección anterior

Próxima clase