Potencias y raíces de números complejos
Potencia n-sima de un número complejo
Para calcular la potencia de un número complejo aplicamos la fórmula de Moivre
por lo tanto
Es decir para elevar a la n-sima potencia un número complejo se eleva a la n-sima potencia el módulo y se multiplica por n el argumento
Ejemplos:
Cálculo de la raíz n-sima de un número complejo
Variando los valores de k se obtienen las n raíces n-simas de un número complejo (un número complejo tiene n raíces n-simas en C).
Ejemplo calcular las raíces cúbicas de -8
Escribimos -8 en forma polar
El módulo de las raíces cúbicas es
Y el argumento
es decir los argumentos son
por lo tanto las tres raíces cúbicas de -8 son
Las podemos expresar en forma binómica
En la siguiente figura se muestran las raíces cúbicas de -8, se observa que una de ellas pertenece a los números reales.
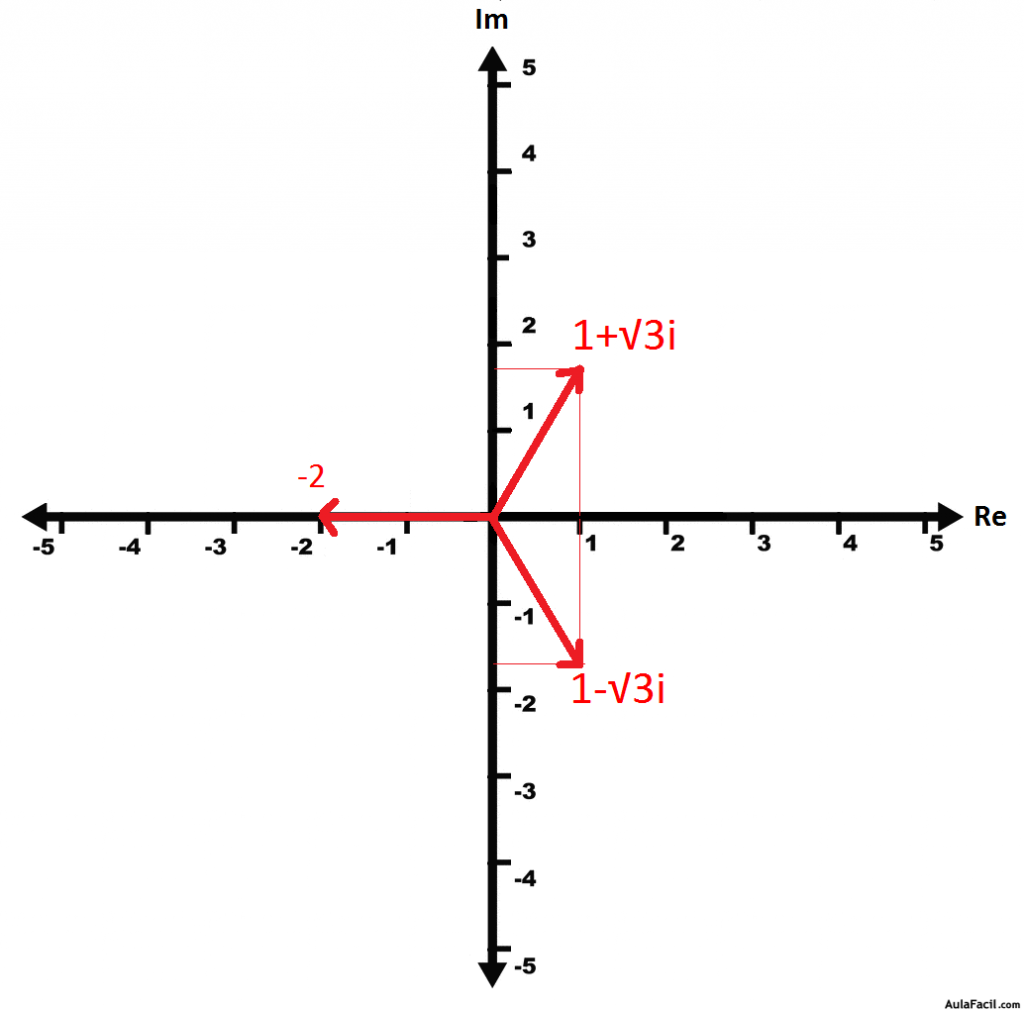
Raíces cúbicas de -8
A continuación se pueden realizar unos ejercicios de autoevaluación
| ||
Corregir
Ver Solución
Limpiar | ||

