Primera Ecuación de Maxwell o ley de Gauss (campo eléctrico)
Si observas el río de la derecha y suponiendo una sección del mismo tal como figura a la izquierda:
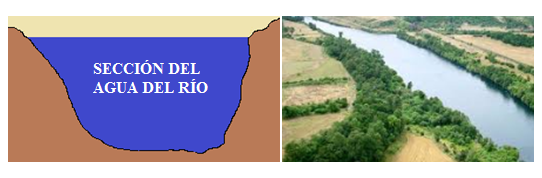
la cantidad de agua que fluye por el punto que consideramos, por unidad de tiempo, depende del Área de la sección y de la velocidad de la corriente de agua.
A mayor velocidad de agua, mayor caudal por unidad de tiempo que pasa por el punto lugar de la observación.
A mayor sección (Área), mayor cantidad de agua por unidad de tiempo.
Lo mismo podemos decir de la ducha que tenemos en casa:
A mayor superficie de agujeros de salida, mayor cantidad de agua sale por unidad de tiempo.
A mayor velocidad de salida del agua, mayor cantidad de agua que fluye.
Viendo las dos últimas fotografías relativas a las duchas, podemos asegurar que la de la derecha tiene mayor paso de agua por unidad de tiempo puesto que sale con mayor velocidad.
En ambos casos, en lugar de hablar de caudal podemos hablar de Flujo (Φ).
Cambiemos el ambiente húmedo por el eléctrico (recuerda que no se llevan bien).
En el caso del Flujo eléctrico a través de una Superficie cerrada consideramos dos casos:
1º: Tenemos una carga eléctrica (positiva) que produce una perturbación en una zona del espacio produciendo un campo eléctrico uniforme de una intensidad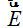 
generando un Flujo cuyas líneas de campo atraviesan una superficie cerrada.
Aunque en el Tema dedicado a la corriente continua ya lo tratamos, ahora insistimos ampliando un poco el concepto de Flujo eléctrico que lo representaremos por Φe.
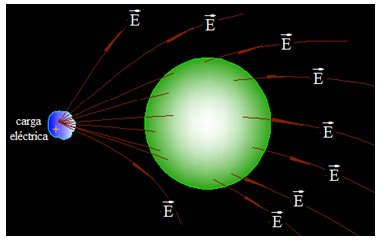
Para hacerlo más sencillo, supongamos que una línea del campo eléctrico procede de una fuente muy lejana por lo que nos llega de forma paralela al plano horizontal:
Tomamos un Área muy pequeña, infinitesimal, con color rojo:
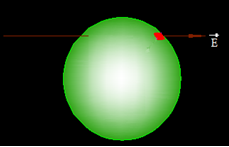
Esta Área tiene el sentido del radio y la aceptamos como valor vectorial representándola con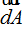 
:
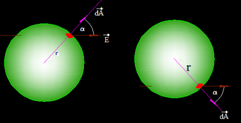
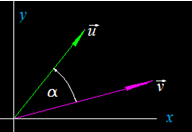
Vemos que el vector Área y vector campo eléctrico forman un ángulo a.
En la última figura hemos señalado un Área muy pequeña con el sentido del radio. A esta Área la hemos representado con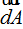 
para indicar, primero, que se trata de un vector y segundo, que es sumamente pequeña, es un Área infinitesimal, un diferencial de A.
Esta Área procede del producto de dos factores, acuérdate del agua que sale de la cabeza de una ducha, decíamos que el Flujo depende directamente del Área de dicha cabeza y de la velocidad del agua.
En el caso del Flujo eléctrico referido a un Área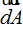 
y una intensidad de campo 
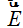será infinitesimalmente pequeño por lo que le representamos con 
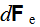(le añadimos el subíndice e por referirnos al campo eléctrico y no perdemos de vista de que se trata de una magnitud escalar) y su valor lo obtendremos de:
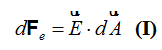
Observa que tenemos el producto escalar (producto punto) de dos vectores.
Sabemos que el producto escalar de dos vectores (lo estudiamos en Matemáticas) equivale al producto de sus módulos por el coseno del ángulo existente entre ellos, es decir: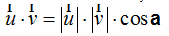
La fórmula (I) podemos escribirla:
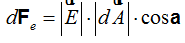
¿Cuántas Áreas tenemos en toda la superficie esférica?
Infinitas.
¿Cómo calculamos el Área de todas ellas?
Sumando todas, integrándolas, de este modo conseguimos calcular el Flujo eléctrico total:
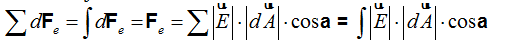
Hemos llegado a: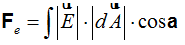 
pero hemos de considerar que la superficie es cerrada, en nuestro caso una esfera por lo que a esta última igualdad la modificamos indicando esta circunstancia (se trata de una superficie total pero cerrada):
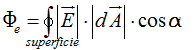
¿Por qué destacamos la circunstancia de que el Área es cerrada?
Observa la figura siguiente donde hemos dibujado varias líneas del campo eléctrico uniforme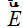 
en puntos distintos de la superficie esférica. Estas líneas entran y salen de la superficie esférica.
En cada punto hemos colocado el valor del ángulo que forman los vectores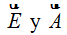 
:
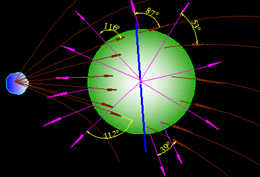
Fíjate bien en la línea azul que divide a la superficie esférica en dos partes. A la izquierda notamos que todos los ángulos superan los 90º mientras que los del lado derecho no llegan a 90º.
Este detalle tiene mucha importancia. Sabemos que el coseno de un ángulo α mientras esté comprendido entre 0º y 90º es positivo y es negativo entre 90º y 180º: cos(180º - α) = - cosα lo que significa que el Flujo correspondiente a la mitad izquierda de la superficie esférica al tener un factor negativo (el coseno de α>90º) tiene un valor negativo.
La mitad derecha de la superficie esférica en el que todos los factores son positivos, el Flujo tiene valor positivo, esto significa que el Flujo total vale 0:
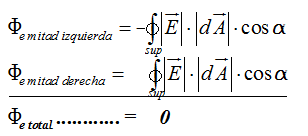
2: La otra posibilidad es que la carga eléctrica se halle dentro de la superficie esférica:
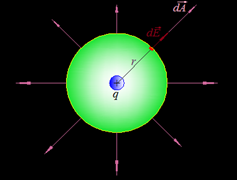
La carga eléctrica situada en el interior de la superficie esférica es positiva por lo que las líneas del campo salen, fluyen hacia el exterior.
Hemos señalado en rojo un diferencial de Área sobre la superficie esférica de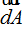 
que es radial (sentido del radio).
La intensidad del campo eléctrico uniforme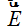 
tiene el mismo sentido que 
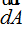por lo que el ángulo entre ambos vectores vale 0.
Volvemos a tomar la fórmula anterior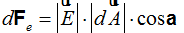 
y recordando lo estudiado en el Tema 6 (Electrostática), dedujimos el valor de la Intensidad:
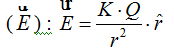
Donde:
Q es el valor de la carga eléctrica
K es la constante de campo eléctrico cuyo valor es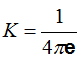 
e es el valor de la permitividad del medio donde se halle la carga y el punto que en nuestro caso es el diferencial del Área que suponiendo sea aire, en este caso, e0 cuyo valor redondeando es: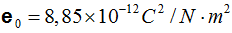 
r es la distancia entre la carga eléctrica y un punto de la superficie esférica cerrada en este caso .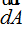
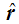es el vector unitario que como sabes es aquél cuyo módulo vale 1 y lo escribimos para que el término de la derecha del signo = adquiera el carácter vectorial puesto que estamos expresando el valor de la Intensidad del campo eléctrico que es también una magnitud vectorial.
El valor de K nos queda:
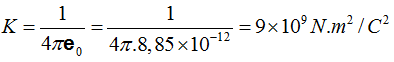
Volviendo sobre la fórmula anteriormente obtenida:
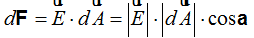
podemos reducirla, teniendo en cuenta que el ángulo α vale 0 (recuerda que ambos vectores son paralelos) y el cos0º = 1 esta fórmula nos queda:
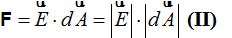(II)
El valor de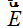 
sabemos que es:
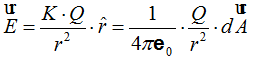
Este valor lo sustituimos en (II):
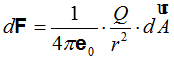
Hemos obtenido la fórmula que nos permite hallar el Flujo correspondiente a una superficie infinitesimal de la superficie esférica.
Para calcular el Flujo correspondiente a toda la superficie esférica no tenemos más que sumar o integrar todas las superficies infinitesimales:
No olvides que estamos tratando con superficies cerradas.
En esta última expresión vemos que la carga Q es una constante, tiene un valor concreto, lo mismo sucede con:
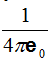no contiene ninguna variable y también r es una constante porque todas las superficies distan de la carga la misma longitud.
A todas estas constantes las sacamos de la integral:
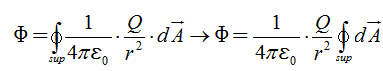(III)
Calculamos la integral de la última igualdad.
¿Cuánto nos da el valor de la suma o integración de todas las áreas infinitesimales?
El Área de la superficie esférica:
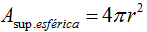
Por lo que la última expresión (III) nos queda:
Al Flujo le hemos colocado el subíndice e para indicar que se trata del Flujo eléctrico.
Como resumen de esta 1ª ecuación de Maxwell decimos que:
Es la Ley de Gauss referida al campo eléctrico y que nos dice que el Flujo eléctrico a través de una superficie cerrada está directamente relacionada con la carga eléctrica que encierra en el interior de la superficie cerrada e inversamente con la permisividad del medio.
