Coeficiente de asimetría
b) Asimetría
Hemos comentado que el concepto de asimetría se refiere a si la curva que forman los valores de la serie presenta la misma forma a izquierda y derecha de un valor central (media aritemética)
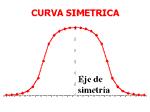
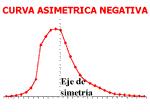
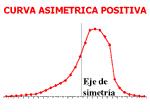
Para medir el nivel de asimetría se utiliza el llamado Coeficiente de Asimetría de Fisher, que viene definido:
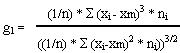
Los resultados pueden ser los siguientes:
g1 = 0 (distribución simétrica; existe la misma concentración de valores a la derecha y a la izquierda de la media)
g1 > 0 (distribución asimétrica positiva; existe mayor concentración de valores a la derecha de la media que a su izquierda)
g1 < 0 (distribución asimétrica negativa; existe mayor concentración de valores a la izquierda de la media que a su derecha)
Ejemplo: Vamos a calcular el Coeficiente de Asimetría de Fisher de la serie de datos referidos a la estatura de un grupo de alumnos (lección 2ª):
Variable | Frecuencias absolutas | Frecuencias relativas | ||
(Valor) | Simple | Acumulada | Simple | Acumulada |
| x | x | x | x | x |
1,20 | 1 | 1 | 3,3% | 3,3% |
1,21 | 4 | 5 | 13,3% | 16,6% |
1,22 | 4 | 9 | 13,3% | 30,0% |
1,23 | 2 | 11 | 6,6% | 36,6% |
1,24 | 1 | 12 | 3,3% | 40,0% |
1,25 | 2 | 14 | 6,6% | 46,6% |
1,26 | 3 | 17 | 10,0% | 56,6% |
1,27 | 3 | 20 | 10,0% | 66,6% |
1,28 | 4 | 24 | 13,3% | 80,0% |
1,29 | 3 | 27 | 10,0% | 90,0% |
1,30 | 3 | 30 | 10,0% | 100,0% |
Recordemos que la media de esta muestra es 1,253
| S((xi - x)^3)*ni | S((xi - x)^2)*ni |
| x | x |
0,000110 | 0,030467 |
Luego:
(1/30) * 0,000110 | ||
| g1 = | ------------------------------------------------- | = -0,1586 |
(1/30) * (0,030467)^(3/2) |
Por lo tanto el Coeficiente de Fisher de Simetría de esta muestra es -0,1586, lo que quiere decir que presenta una distribución asimétrica negativa (se concentran más valores a la izquierda de la media que a su derecha).
