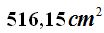Áreas de los Cuerpos Geométricos - Áreas de los Poliedros Regulares
Anteriormente estudiamos las áreas de las figuras planas. En este tema nos dedicaremos a estudiar las superficies que envuelven a los cuerpos geométricos o cuerpos sólidos.
Entendemos por cuerpo sólido al que ocupa un lugar en el espacio. Es decir, el que contiene las tres dimensiones (largo, ancho y alto).
Si este sólido tiene forma de poliedro, prisma o cuerpo redondo podemos referirnos a los cuerpos geométricos.
ÁREAS DE LOS POLIEDROS REGULARES
Recordarás que estudiamos los volúmenes de los cinco poliedros regulares. Ahora estudiaremos el cálculo de sus superficies.
Los poliedros regulares tienen todas sus caras iguales:
1) Tetraedro.- Sus cuatro caras son triángulos equiláteros.
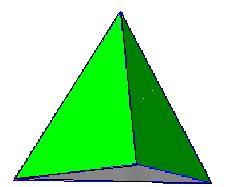
El área total de este cuerpo geométrico lo hallaremos calculando el área de una cara y la multiplicaremos por 4.
Para este cálculo necesitamos conocer la apotema o altura de una cara de un poliedro.
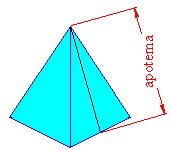
La altura de una cara la calculamos a partir de la figura siguiente:
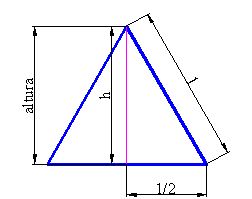
A la arista o lado del triángulo le damos el valor 1 para facilidad de cálculo y no tener que aprender fórmulas.
En cada caso, aplicamos los conocimientos básicos de geometría con un poco de sentido común.
Primeramente calculamos la altura que la representaremos con h.
La hipotenusa vale 1 y un cateto (mitad de la base que mide 1/2). Utilizando el teorema de Pitágoras tendremos:
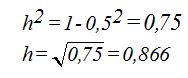
El área de una cara para cuando la arista vale 1 será:
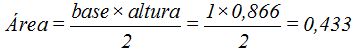
Cuando el lado del triángulo o arista de una cara valga a el área será:
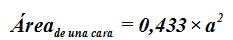
La arista la elevamos al cuadrado por tomarla en dos dimensiones: largo y ancho 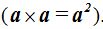
Como el tetraedro tiene 4 caras, la superficie total será: 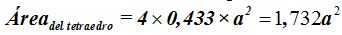
15(4).1 Halla la superficie total de un tetraedro de 5 cm., de arista.
Respuesta: 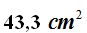
2) Octaedro.- Sus 8 caras iguales son triángulos equiláteros.
Cada triángulo equilátero del tetraedro de lado 1, hemos visto que tiene una superficie de 0,433.
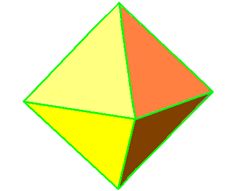
Como el octaedro tiene 8 caras multiplicaremos la superficie anterior por 8 y por el valor del cuadrado del lado del triángulo o arista de dicho octaedro:
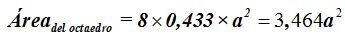
15(4).2 Calcula el área total de un octaedro de 5 cm. de arista:
Respuesta: 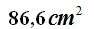
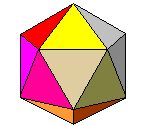
3) Icosaedro.- Sus 20 caras iguales son triángulos equiláteros.
Dado que cada cara tiene una superficie de 0,433 siempre que el lado mide 1, la superficie total de esta figura será:
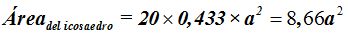
15(4).3 Calcula el área total de un icosaedro de 5 cm. de arista.
Respuesta: 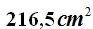
4) Cubo.- Sus 6 caras son cuadrados iguales. El área de cada cara será el valor del lado por sí mismo, es decir;
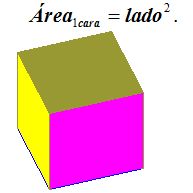
El área total del cubo será, llamando a al valor del lado del cuadrado o arista del cubo:
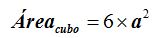
15(4).4 Calcula el área total de un cubo de 5 cm. de arista.
Respuesta: 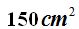
5) Dodecaedro.- El dodecaedro está compuesto por 12 pentágonos iguales y dedujimos en el Tema 15(3) que el área de uno de ellos de lado a o arista del dodecaedro es:
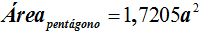
Para saber el área total de un dodecaedro multiplicaremos el área de una cara por 12:
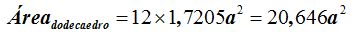
15(4).5 Calcula el área total de un dodecaedro de 5 cm. de arista.
Respuesta: