Traslaciones en el Plano
El hecho de cambiar de posición una figura en un plano llamamos traslación. Se trata de trasladar una figura a un lugar del plano a una distancia, dirección y sentido determinados.
8.18 Realizar la traslación de un triángulo a otro lugar del plano tomando como guía un vector.
Solución:
Vas a ir haciendo paso a paso lo que se te va indicando:
Solución:
Vas a ir haciendo paso a paso lo que se te va indicando:
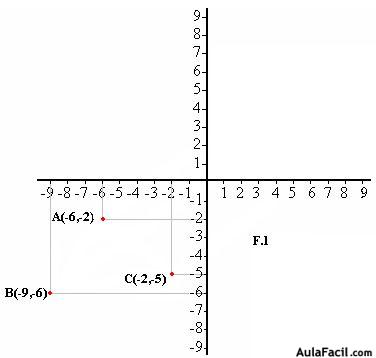
1º En una hoja de papel cuadrícula dibuja un eje de coordenadas como tienes en F.1.
Señala los puntos: (-6,-2), (-9,-6) y (-2,-5) que serán los vértices del triángulo
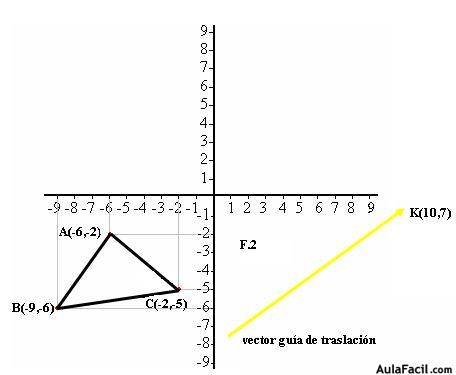
2º Unes los puntos ABC del triángulo y dibujas un vector guía de traslación, lo tienes en color amarillo. Observa que el extremo de este vector tiene de componentes (10,7).
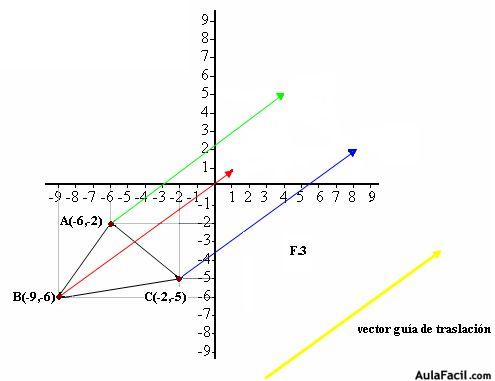
Un modo sencillo de hacer una traslación es servirnos del vector guía. Para ello, a cada punto ABC del triángulo le colocamos el vector guía guardando el mismo módulo, dirección y sentido del vector guía tal como lo tienes en F.3 con los colores verde, rojo y azul.
Un modo sencillo de hacer una traslación es servirnos del vector guía. Para ello, a cada punto ABC del triángulo le colocamos el vector guía guardando el mismo módulo, dirección y sentido del vector guía tal como lo tienes en F.3 con los colores verde, rojo y azul.
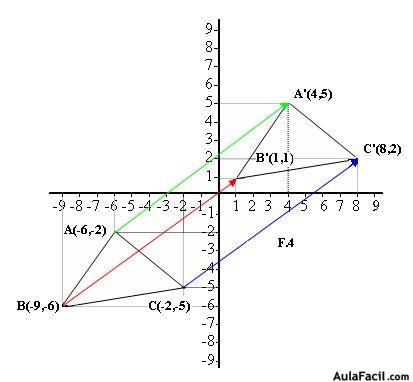
Los extremos de cada uno de los vectores verde, rojo y azul son los nuevos vértices del triángulo.Si sumas las componentes de cada punto A, B y C con los del vector guía tendrás los puntos correspondientes al nuevo triángulo.
F.4.
El triángulo ABC se ha convertido en el A’B’C’ de acuerdo con el vector guía.
Así pues, los vectores que unen los puntos ABC con A’B’C’ tienen el mismo módulo, dirección y sentido.
Los puntos A’,B’ y C’ son los homólogos de A, B y C, es decir, que están colocados en el mismo orden o posición.
Si sumamos las componentes del punto A = (–6, –2) con las del vector guía (10,7) obtenemos las componentes del punto A’ (–6 + 10, –2 + 7) = A’(4,5)
Si sumamos las componentes del punto B = (–9, –6) con las del vector guía (10,7) obtenemos las componentes del punto B’ (–9+ 10, –6+ 7) = B’(1,1).
Si sumamos las componentes del punto B = (–9, –6) con las del vector guía (10,7) obtenemos las componentes del punto B’ (–9+ 10, –6+ 7) = B’(1,1).
Si sumamos las componentes del punto C = (–2, –5) con las del vector guía (10,7) obtenemos las componentes del punto C’ (–2+ 10, –5+ 7) = C’(8,2)